Brock Engineering
P. O. Box 302, Roxbury CT 06783 (860) 354-7069
COMBINED DISCRETE-CONTINUOUS SIMULATION MODELS IN PROMODEL FOR WINDOWS
J. Frederick Klingener klingener@BrockEng.com
President, Brock Engineering, P.C.
Roxbury, Connecticut 06783, U.S.A
Proceedings of the 1995 Winter Simulation Conference pp.
445-450
ed. C. Alexopoulos, K. Kang, W. R. Lilegdon, and D. Goldsman
Presented at the 1995 Winter Simulation Conference, December 3-6, 1995, Arlington, Virginia
ABSTRACT
Although ProModel for Windows is primarily intended as a discrete event simulator aimed at part manufacturing systems, it supports construction of models that combine continuously varying processes that interact with discrete events. This paper proposes a general approach to modeling of combined discrete-continuous systems, describes the details of a particular example problem, and discusses some modeling issues.
1 BACKGROUND AND PURPOSE
Simulation of continuously varying systems or of combined discrete-continuous system gets short shrift in the basic texts. Law and Kelton (1991) have a subsection called "Other Types of Simulation." and devote three pages to it, identifying SIMAN, SIMSCRIPT, and SLAM II as suitable for building combined models. They describe the following three types of interactions that may arise in combined models: (1) a discrete event may cause a discrete change in the value of a continuous state variable, (2) a discrete event may cause a relationship governing a continuous state variable to change at a particular time, and (3) a continuous variable achieving a threshold value may cause a discrete event to occur or be scheduled. This paper describes an approach for incorporation of interacting continuous processes into a discrete event simulation model.
ProModel for Windows, a tool for simulating and analyzing production systems, is intended primarily for modeling discrete part manufacturing systems. In ProModel, a simulation is event-driven - the basic events being the arrival of Entities at Locations. These basic events cause the execution of code blocks that describe the Processing (the Operations performed there and the subsequent Routing of the Entities to other Locations). The mechanics of model building in ProModel consist primarily of specifying code blocks that define the passage of materials through the system, sandwiched between initialization and termination routines. The programming language is procedural, has primitive but useful data structures, and provides conditional branching within a block. There is no explicit provision for looping or recursion.
The purpose of this paper is to show how ProModel for Windows can be used to construct combined discrete-continuous simulation models.
2 METHOD
A general equation that governs a continuous state variable, y(t), can be written in the form:
dy/dt = f(y,x,t)
where dy/dt is the derivative of y with respect to time, t, and x represents the other state variables that define the system. For numerical evaluation, this relationship can be approximated by:
{delta}y = f(y,x,t) {delta}t
where {delta}y and {delta}t are finite changes in y and t. The value of y at a time of t+{delta}t can be written as Equation (1):
y(t+{delta}t) = y(t)+{delta}y = y(t)+f(y, x, t){delta}t (1)
The method for incorporating continuous processes into ProModel rests on: (1) the expression of continuous state variables as (global) Variables or (Entity or Location) Attributes, (2) formulation and numerical integration of the equations of state for those variables, and (3) ensuring proper interaction between the continuous and discrete state variables. There are two critical features of ProModel that enable the method: (1) the ability to hold up Operations on an Entity at a Location by including a WAIT UNTIL statement that can be made conditional on the value of a global Variable or an accessible Attribute, and (2) the ability to write recurring blocks of general procedural programs that can read the condition of the discrete system variables and read and change the values of global Variables and Attributes.
Table 1 shows the outline of one method for maintaining a continuous state variable in ProModel. When Ent1 arrives at Loc1, it causes a single execution of the Operation block. After a delay of dt, Ent1 is routed back to Loc1. For a state variable Var1, a defined time step, dt, and f, an expression for the time rate of change of Var1, the Operations block implements Equation (1) for Var1 repetitively throughout the simulation. The effect of discrete system changes on the rate of change of Var1 is expressed in f. If Var1 is declared as a global variable, then its value can be used to affect other operations, and the variable Var1 can, itself, be changed directly by other continuous or discrete operations.
| PROCESS | ROUTING | ||||
| Entity | Location | Operation | Output | Destination | Rule |
| Ent1 | Loc1 | Var1 = Var1 + f(Var1,x,t) x dt | Ent1 | Loc1 | CONTINUE 1 |
| WAIT dt |
3 EXAMPLE PROBLEM
A statement of some disclaimers is necessary before the example is described in detail. First, the model described here was implemented on version 1.05 of ProModel. Although recent versions of this software give more direct support for the techniques described here, the earlier version is adequate for illustrative purposes. Second, the arrangement described is only one of several equally valid possibilities. In particular, some features of the model are structured principally to illustrate the versatility of the modeling package. Third, the model uses a simple numerical integration technique that is valid only in very simple problems, but the method can be extended for practical problems in ways that Section 4 discusses.
This section describes the formulation of a model described in Law and Kelton (1991). They describe an oil tanker transport model in which discrete events, such as tanker arrivals and departures, depend on threshold levels reached by continuously varying quantities, such as the fill levels of storage tanks. The model was originally fully specified in Pritsker (1986) as an example problem to be implemented in SLAM II.
3.1 Problem Description
As an example of a combined discrete-continuous system, Pritsker (1986) specifies the following problem:
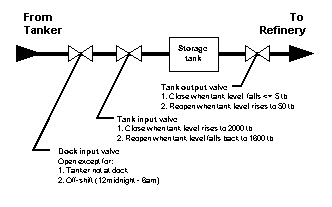
A fleet of 15 tankers carries crude oil from Valdez, Alaska to an unloading dock near Seattle, Washington. It is assumed that all tankers can be loaded simultaneously in Valdez, if necessary. In Seattle, there is only one loading dock, which supplies a storage tank that feeds a refinery through a pipeline. The storage tank receives crude from a tanker at the dock at a constant rate of 300 tb/day (thousand barrels/day). The storage tank supplies crude to the refinery continuously at a constant rate of 150 tb/day. The unloading dock is open from the hours of 6 am to 12 am [midnight]. Safety considerations require the stopping of tanker unloading of the crude when the dock is shut down. The completion of tanker unloading occurs when the amount of crude remaining in the tanker is less than 7.5 tb.
The storage tank has a capacity of 2000 tb. When it is full, unloading is halted until the amount in the tank decreases to 80 percent of capacity When the storage tank is nearly empty (less than 5 tb), supply to the refinery is halted until 50 tb is reached to avoid the possibility of frequent refinery start-ups and shut-downs. The characteristics associated with the tankers are listed below.
The initial conditions for the simulation are that the storage tank is half full and the tankers are to arrive at their loading points and ½ day intervals, starting with the first at time 0.
3.2 Model Description
The model uses one real Entity type - tanker, the oil
tanker, three real Locations - Valdez, Seattle_ harbor,
and Seattle_dock., and two continuous state Variables
- tanker_contents (the level of oil in the tanker at
Seattle_dock), and tank_ contents (the level
of oil in the dock storage tank) expressed as global Variables.
Table 2 shows the initialization block for the model variables.
| #--CONSTANTS-------------------------------- | |||||||
| # CAPACITIES | |||||||
| tanker_capacity = 150.0 | # tb | ||||||
| tanker_heel = 7.5 | # tb | ||||||
| tank_high_high = 2000.0 | # tb | ||||||
| tank_high = tank_high_high * 0.80 | |||||||
| tank_low = 50.0 | # tb | ||||||
| tank_low_low = 5.0 | # tb | ||||||
| # FLOW RATES | |||||||
| tanker_pump_rate = 300.0/24.0 | # tb/hr | ||||||
| refinery_input_rate = 150.0/24.0 | # tb/hr | ||||||
| # INTEGRATION TIME STEP | |||||||
| dt = 0.4 | # hr - gives tol. of 5 tb at 300 tb/day | ||||||
| #--STATE VARIABLES-------------------------- | |||||||
| # LOGICAL | |||||||
| dock_input_valve = Closed | |||||||
| tank_input_valve = Closed | |||||||
| tank_output_valve = Closed | |||||||
| # CONTINUOUS | |||||||
| tank_contents = tank_high_high/2.0 | |||||||
| tanker_contents = 0.0 | |||||||
Figure 1 shows the schematic arrangement of the dock pipe connections and valves between the tanker and the refinery. The figure also defines, for each valve, the interaction between its alignment and the system state variables. These interactions are coded into Subroutines, one example of which is shown in Table 3. To ensure that the interactions between the discrete and continuous processes are completely expressed, the Subroutines are called by the Operations blocks of the dummy Entities at each integration time step.

| LOGIC | ||||||
| IF current_state = Closed | ||||||
| THEN IF tank_contents <= tank_high | ||||||
| THEN RETURN Open ELSE RETURN Closed | ||||||
| ELSE IF tank_contents>=tank_high_high | ||||||
| THEN RETURN Closed ELSE RETURN Open | ||||||
| Entity | Location | Operation |
| Tanker | Valdez | 24.0*U(30,0.1) #uniform distr. 3 da. Mean, 0.1 da half-span |
| Tanker | Seattle_harbor | # no operation - just wait for dock space |
| Tanker | Seattle_dock | tanker_contents = tanker_capacity # reset the state variable |
| WAIT UNTIL tanker_contents <= tanker_heel | ||
| Euler | Euler_loc | USE dock_workers, 5 for dt |
| dock_input_valve = realign_dock_valve(dock_input_valve) | ||
| IF (dock_input_valve = Open) AND (tank_input_valve = Open) THEN {tanker_contents = tanker_contents - tanker_pump_rate * dt | ||
| tank_contents = tank_contents + tanker_pump_rate * dt } | ||
| Euler2 | Euler_loc | tank_input_valve = realign_tank_input_valve(tank_input_valve) |
| tank_output_valve = realign_tank_output_valve(tank_output_valve) | ||
| IF tank_output_valve = Open THEN tank_contents = tank_contents - refinery_input_rate * dt | ||
| WAIT dt |
One dummy Entity, Euler, is used to integrate the equations governing the level of oil in the tanker and to manage the interactions with other system variables, and another, Euler2, is used for the level of oil in the dock storage tank. The dummy Entities are programmed to Arrive at a Location at the beginning of the simulation, to execute their Operations blocks that implement the numerical integration of the state equations, to wait for a specified integration time step, and finally to re-enter the same Location using a CONTINUE routing to repeat the process through the entire simulation time. Table 4 shows the Operations blocks for the integrating Entities.
The motivation for using two Entity types was to illustrate how ProModel Resource scheduling can be used to control part of the integration. Tanker unloading was controlled by: (1) defining a resource named dock_workers, (2) using ProModel's shift editor to define the hours that the resource would be available, and (3) specifying that Euler USE the dock_workers (rather than the simple WAIT, specified for Euler2) for a duration of dt. Because of this difference, numerical integration of the equation governing tanker contents proceeds only during on-shift hours, while integration of the equations governing storage tank unloading proceeds continuously throughout the simulation.
4 RESULTS
Figure 2 shows the values of selected state variables as functions of simulation time. This figure is produced by programming ProModel to create an external data file and to write evolutionary results to it (the code to do this data reporting is a part of the operations and routing instructions that are omitted for clarity from the listings in Tables 1 through 3.) An external post processor (not part of ProModel for Windows) is used to organize and to display the results. The figure shows example traces as function of simulation time for three types of state variables continuous, step, and logical:
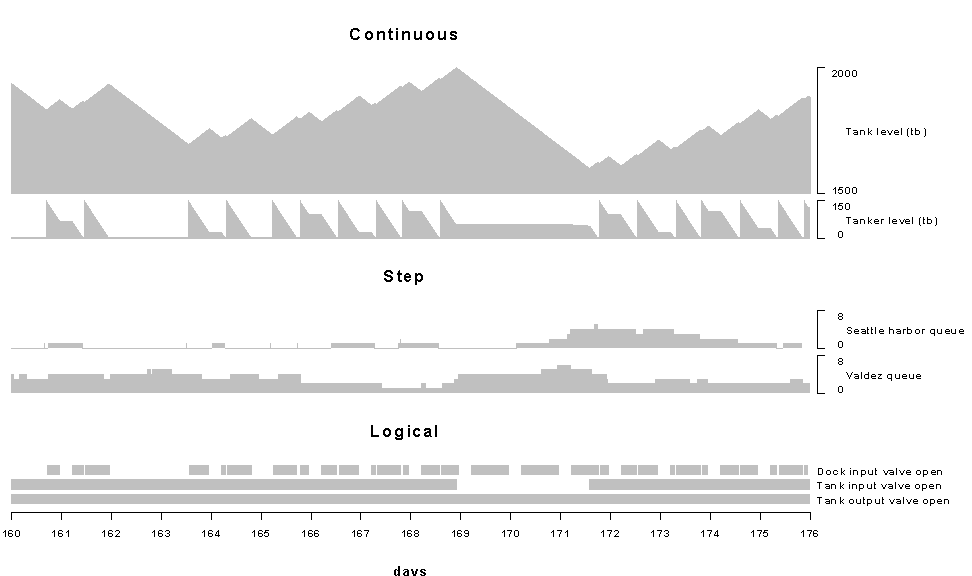
1. Continuous. The two top traces show the contents of the storage tank and of the tanker at the Seattle unloading dock as (piecewise) continuous functions of time. The contents of the tanker is reset to 150 tb (the tanker capacity) when a tanker arrives at the dock, and it decreases until it is empty. The decrease is continuous except when the dock input valve is closed or when the tank input valve is closed. The top trace shows that the storage tank level increases during periods of tanker unloading and decreases when the dock input valve is closed. At approximately 168 days, the storage tank becomes full, the tank input valve closes, and tanker unloading stops. These traces show changes in the values of continuous state variables in response to normal continuous processes, to the discrete events, and to threshold events in the continuous variables.
2. Step. The two traces directly below the continuous state traces show the number of tankers loading at the Valdez port and lying in the Seattle harbor awaiting space at the unloading dock. These step traces show changes in the values of discrete state variables in response to the discrete events of tanker arrivals and departures.
3. Logical. The states of the valves as functions of time, open or closed, are shown in the three traces at the bottom of the graph. A blank space indicates that the valve was closed for the corresponding time, and a shaded portion indicates that the valve was open. The tank output valve was open for the duration displayed; the tank input valve was open except for the period beginning late on day 168 (when the tank level reached its maximum permissible level of 2000 tb) and ending in the afternoon of day 171 (when the tank level had been drawn down to 1600 tb); the dock input valve trace shows the valve operating as specified - closing for the off-shift periods between midnight and 6 am each day and closing during the periods when there was no tanker present at the dock. These traces show changes in the values of logical (Boolean) state variables in response to discrete events and to threshold events in the continuous variables.
Section 1 enumerated three types of interaction among state variables in a combined discrete-continuous system, and Figure 2 illustrates examples of each type in the tanker model. First, the arrival of a laden tanker at the unloading dock (a discrete event) resets the level of the tanker contents (a continuous variable) to 150 tb. Second, changes in valve positions (discrete events) change the pump flow rates into and out of the storage tank. These flow rate changes alter the relationships governing the tank and tanker level (continuous variables.) Third, when the tank level (a continuous variable) reaches its high cutoff point it causes the tank input valve to close (a discrete variable.)
5 MODELING ISSUES
Although ProModel for Windows permits implementation of combined discrete-continuous models, the analyst is left to deal with modeling issues that are familiar to anyone who has worked in programming or numerical analysis. These issues include: (1) selection of data structures, (2) selection and evaluation of numerical integration schemes, (3) arrangement of data logging methods, (4) selection of integration time step size. This section discusses each of these issues.
5.1 Data Structures
In the early versions of ProModel, selection among possible data structures is simple, because of limited choice - there are only two general types of variables available to the user: (global) variables and (local) attributes that can belong to entities or locations. Unless the form of the model strongly suggests one form or another (different tanker capacities among the fleet in the example problem would argue strongly for maintaining tanker capacities as entity attributes) then the selection is based mainly on programming style, following the rule to localize a variable's scope to the greatest extent possible.
5.2 Numerical Integration Schemes
For clarity, the example problem uses a simple Euler method that predicts the value of a function at the end of a time step based solely on its value and derivative evaluated at the beginning. Because of the simplicity and the predictability of the example model's interactions, the technique probably gives adequate results in this case. However, real applications would require more robust methods, such as an implementation of Runge-Kutta, a technique that is based on evaluating the function and its derivatives at several places within a time step and combining the results in a way that minimizes the error. The method is described in Press, et al. (1992), and the programming examples given there can be readily recast into ProModel language. In a discussion of the relative merits of the Euler method, Press recommends that the Euler method is not suitable for practical use because of its relative inaccuracy and relative instability. Stability is of particular concern in the modeling of combined discrete-continuous systems because of the abrupt changes in the state equations. Press, et al. (1992) suggest that the fourth order Runge-Kutta procedure "does an excellent job feeling its way through rocky or discontinuous terrain."
The computational overhead of the Runge-Kutta methods can be partially offset by dynamically adjusting the integration time step size in response to the state of the system at any given time. It is hard to improve on Press' imagery: "Many small steps should tiptoe through treacherous terrain, while a few giant strides should speed through smooth uninteresting countryside." Because system state variables are available to ProModel's code blocks, local or global time step sizes can be adjusted to respond to predicted or past discontinuities.
5.3 External Data Logging
By introducing model elements (the continuous state variables) that are maintained, at least in part, by the user's code, the user may lose some of the desired statistical analysis normally a part of ProModel output, and this supplementary analysis may have to be arranged by external programs. ProModel supports this supplementary analysis by permitting data writing to external files, but volume and size of files become an issue. Writing values of continuously varying state variables to an external file at each integration time step may result in impractical volumes of data. For this reason, the data logging period should be adjusted along with the integration step size.
5.4 Integration Time Step
Selection of a proper integration time step size requires finding a balance between satisfactory resolution (prevention of overshoot in any of the continuous state variables), convergence, and stability on the one hand and the practical use of computer resources of execution time and data storage on the other. In the example problem, the required resolution was specified, and the model interactions were simple enough that a static maximum time step could be calculated. In addition, because of the simplicity of the structure of the example problem, there was no tendency toward instability. In a practical case, however, careful experimentation is required.
ACKNOWLEDGMENTS
The author thanks Pritsker Corporation for providing a copy of the SLAM II manual and thanks Scott Macrae for his technical review and helpful comments.
REFERENCES
AUTHOR BIOGRAPHY
J. FREDERICK KLINGENER is president of Brock Engineering,
P. C. in Roxbury Connecticut. He received a B. S. in 1962 and
an M.S. in 1966 in mechanical engineering from Carnegie Institute
of Technology. He is a registered mechanical engineer in the state
of Alaska. He has had broad experience in design, analysis, and
fabrication of nuclear, robotic, and automotive mechanical systems.
He has recently worked in cost, risk, and production analysis
of the army's program to dispose of unserviceable chemical weapons.
Mr. Klingener's current interests include data analysis of real
and simulated manufacturing processes.
Return to the top of
the Brock Engineering home
page.
Your comments and suggestions are welcomed at klingener@BrockEng.com
or at (860) 354-7069
| REVISION HISTORY | ||||||
| content | 08-10-95 | submit camera-ready draft | ||||
| html | 09-17-96 | format for html | ||||
| 02-01-98 | revise for new site | |||||